2019 m. birželio mėn. 19 d., trečiadienį, 16:15-16:30, 416 aud., LKA ramovė, Šilo g. 5A, Lietuvos matematikų draugijos 60-oji konferencija, programa.
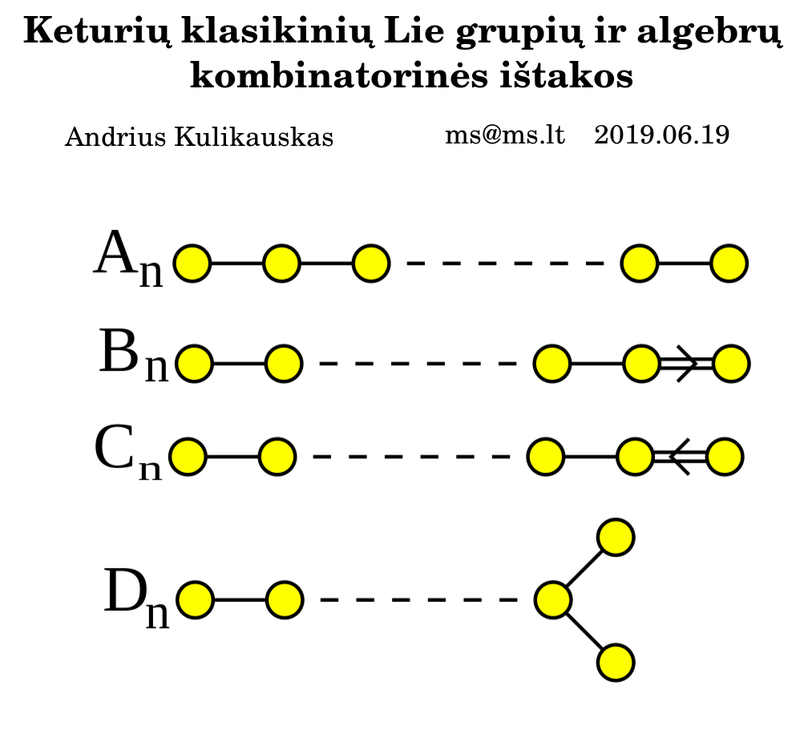
Keturių klasikinių Lie grupių ir algebrų kombinatorinės ištakos
Esu filosofas. Vaikystėje užsimojau viską žinoti ir tą žinojimą gražiai taikyti. Besąlygiška tiesa išsakytina sandaromis, o matematika yra sandarų mokslas. Tad 1993-čiaisiais metais būtent iš matematikos, algebrainės kombinatorikos, gavau daktaro laipsnį iš Kalifornijos universiteto San Diege.
Prieš trejus metus pasiryžau atsekti, kokiais samprotavimais išsivysto visa matematika, jos paskiros šakos, sąvokos, klausimai, atsakymai, tyrimo būdai. Pradžiai pasidariau matematikos šakų klasifikacijos žemėlapį, pamąsčiau kuri šaka kuria remiasi. Bendrais bruožais, matematika plasnoja dviem sparnais, analize ir algebra, kuriuos sieja daugiamatė geometrija. Analizės ir algebros sąsają išsako atitikimas tarp kompaktinių Lie grupių ir paprastųjų Lie algebrų. Iš esmės, kompaktinė Lie grupė yra matricų grupė išreiškianti daugiamačius posūkius, o paprastoji Lie algebra yra tų posūkių ašių sankabų simetrijų lentelė. Šios erdvės ir simetrijos riboja įmanomas geometrijas ir sudaro teoretinės fizikos abėcėlę.
Lie teorija yra, mano galvai, siaubingai miglotos bendrybės, tačiau jos išdavos yra stebuklingai dalykiškos. Galimybes išsako pavaizduotos Dynkin diagramos. Yra keturios begalinės, klasikinės šeimos ir penkios papildomos išimtys. Mane domina, kaip paprasčiausiai suprasti ir paaiškinti, kuomi pasižymi šios klasikinės šeimos ir kodėl jų yra būtent keturios.
Išmąsčiau, kad keturios klasikinės šeimos išsako simetrijas slypiančias pačioje matematikoje, tai yra, glūdinčios mąstant bet kurią sandaugą, bet kurią pasirinkimų grandinę. Pristatysiu keturis skirtingus būdus, kaip galime mąstyti pasirinkimų grandinę.

Pirmiausia atkreipiu dėmesį, kad matematikoje susiduriame su dviem skirtingomis priešingybių rūšimis, simetriškomis priešingybėmis ir nesimetriškomis priešingybėmis. Nesimetriškos priešingybės pavyzdys yra kada renkamės dauginti iš 1 arba -1. Mes galime atskirti šias dvi galimybes, nes {$1 \times 1 = 1$}, tuo tarpu {$-1 \times -1 \neq -1$} bet {$-1 \times -1 = 1$}. Užtat yra pagrindas vieną priešingybę nepažymėti, o kitą priešingybę pažymėti, kaip jos neigimą.
Tuo tarpu skaičiaus {$-1$} dvi šaknys, i ir j, yra iš esmės neatskiriamos. Nėra vidinio pagrindo atskirti posūkį į kairę nuo posūkio į dešinę. Juk {$i \times i = j \times j = -1$}. Tai yra du jungtiniai ir negalime pasakyti, kuri šaknis vadintina i ir kuri vadintina j. Užtat pedagogiškai save labai klaidiname kai tas šaknis vadiname i ir -i, tarsi viena būtų pagrindinė o kita šalutinė, juk kokybiškai jos visiškai nesiskiria, tuo tarpu 1 ir -1 skiriasi.
Jeigu nori, kad mergytė valgytų, turi jai duoti simetrišką pasirinkimą: ar nori valgyti dešrelę ar bananą? Jeigu paklausi nesimetriškai, ar nori valgyti? tai gali visai nevalgyti. Jeigu neturi pinigų, tai rašyk nulį, o tai bus simetriška milijonui. O jeigu nieko nerašysi, tai tavo nulis bus nesimetriškas tam milijonui. Būti ar nebūti yra nesimetriška priešingybė, būti vienokiu ar kitokiu yra simetriška priešingybė. Ši plonybė pasireiškia mąstant kintamųjų sandaugas, jas modeliuojant binomo teorema, Paskalio trikampiu, ir skirtingai interpruojant politopais.
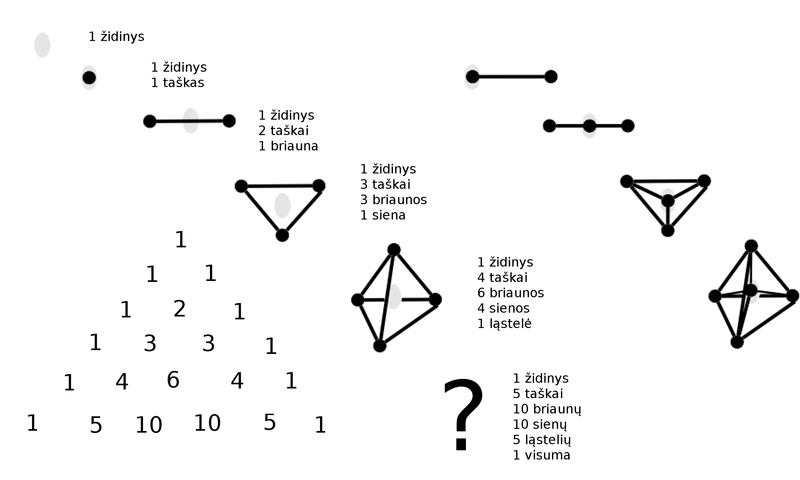
Viena politopų šeima yra simpleksai, kuriuos galime generuoti taip. Pradėkime nuo tuščio židinio ir duokime tam židiniui vis pagimdyti po vieną viršūnę. Viena viršūnė, tai taškas. Iš židinio išskiriant antrą viršūnę, gauname tiesės atkarpą, ir židinys pasislenka. Pagimdžius trečią viršūnę išvystame trikampį, pagimždius ketvirtą viršūnę - tetrahedrą su keturiais trikampiniais šoniais. Paskalio trikampis atskleidžia iš ko šie simpleksai susideda. Trikampis turi vieną židinį, tris viršūnes, tris kraštines ir vieną visumą. Tetrahedras turi vieną židinį, keturias viršūnes, šešias kraštines, keturis šonus ir vieną visumą. Ir jeigu savo vaizduote patampytumėme tetrahedro židinį, įsitikintumėme, kad ketvirtamatis simpleksas susidarys iš vieno židinio, penkių viršūnių, dešimt kraštinių, dešimt šonų, penkių tetrahedrų ir vienos visumos. Noriu atkreipti dėmesį, kad kiekviename simplekse, pavyzdžiui, trikampyje, židinys ir visuma yra nesimetriškos priešingybės, mat, židinys susidaro iš jokių viršūnių, o visuma susidaro iš visų viršūnių. Tai yra ne šiaip semantinis skirtumas, kaip ką pavadiname, o sintaktinis skirtumas tarp to kas yra ir to ko visiškai nėra.
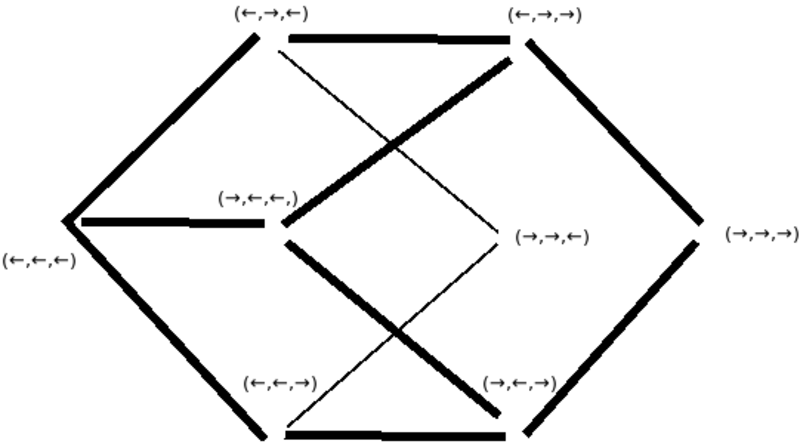
Simetriškas priešingybes vaizduoja koordinačių sistemos. Koordinates išsakysiu strėlėmis, į kairę ir į dešinę, kad jų simetriškumas būtų akivaizdus. Kubo aštuonios viršūnės išsidėsto pagal Paskalio trikampį. Kubą galime atitinkamai supjaustyti. Šitaip mąstant kubas nėra politopas, jis nesusideda iš politopų, nėra židinio, nė visumos. Šis kūbas susideda iš ašių, tad jo viršūnės yra savybių rinkiniai. Kiekvienu klausimu, kiekviename mate, kiekvienoje ašyje pasirinkta vienaip arba kitaip. Užtat sukeitus visas strėles į kairę ir į dešinę niekas iš esmės nepasikeistų, nes tai iš tiesų tėra semantinis skirtumas, priklausantis nuo visuminio konteksto, ką reiškia strėlė į kairę ir strėlė į dešinę. Užtat tokios koordinačių sistemos simetrijų grupę tenka padalinti iš dviejų. Simplekso simetrijas išsako simetrinė grupė, o koordinačių sistemos simetrijas išsako [hiperoktahedrinės grupės pogrupė].
Kvantinei fizikos šios plonybės turėtų būti svarbios nes jos skiria stebinį ir stebėtoją. Gamtoje visada būna arba vienaip arba kitaip. Gamtoje tarpų nebūna. O stebėtoja stebi, kas įvyks tam tikru metu, jinai atrėžia stebėjimo tarpus. Stebėjimo tarpe gali kažkas įvykti arba neįvykti, būti arba nebūti. Stebėtojas plėtoja nesimetriškas priešingybes, o stebinys plėtoja simetriškas priešingybes.
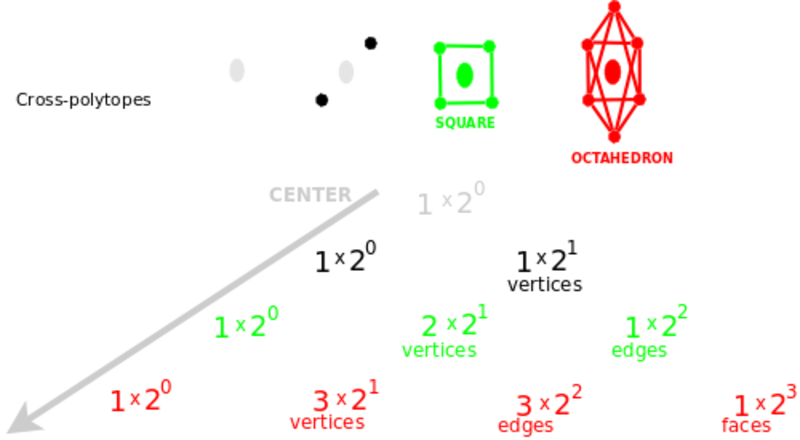
Yra dar du mišrūs pasirinkimai, kuriuos išsako kryžminiai politopai ir hiperkubai. Įsivaizduokime, kad židinys gimdo viršūnes poromis, tarsi teigiamas ir neigiamas dalelytes, skriejančias priešingomis kryptimis, ištiesiančias ašis arba tieses. Tuomet Paskalio trikampį galima suvokti, kaip siejantį ašis. Oktahedrą sudaro trys ašys. Jisai turi vieną židinį, tris kart du, tai yra, šešias viršūnes, tris kart keturias, tai yra, dvylika kraštinių, ir aštuonis šonus. Įsidėmėkime, kad Paskalio trikampis tvirtina, kad oktahedras neturi visumos, neturi tūrio! Užtat jisai turi aštuonis orientuotus šonus, kuriais skiria vidų ir išorę.
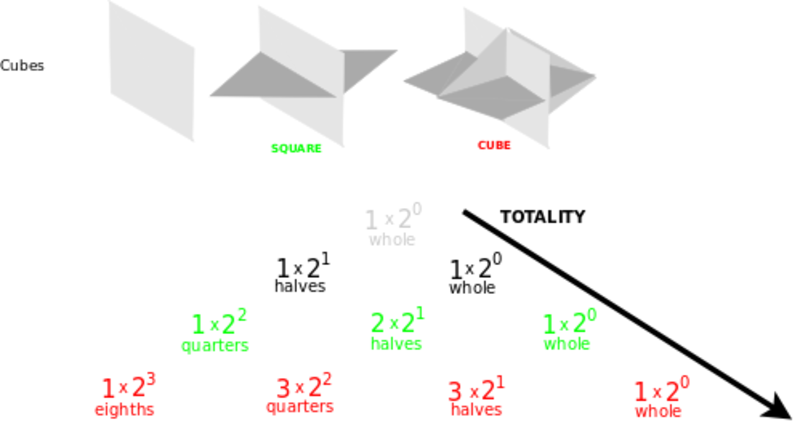
Kryžminio politopų dualas yra hiperkubai. Hiperkubas susidaro iš erdvės skaidymų. Pavyzdžiui, kubas turi vieną visumą, tris kart du šonus, tris kart keturias kraštines, ir aštuonias viršūnes. Užtat viską skaidantis hiperkubas neturi židinio.

Viską apžvelgus, besirenkantis protas gali ketveriopai nusiteikti:
- simpleksais: parinkti ar neparinkti
- kryžminiais politopais: pasirinkti vienaip ar pasirinkti kitaip ar neparinkti
- hiperkubais: parinkti ar nepasirinkti vienaip ar nepasirinkti kitaip
- koordinačių sistemomis: pasirinkti vienaip ar kitaip - arba tolygiai - nepasirinkti vienaip ar nepasirinkti kitaip
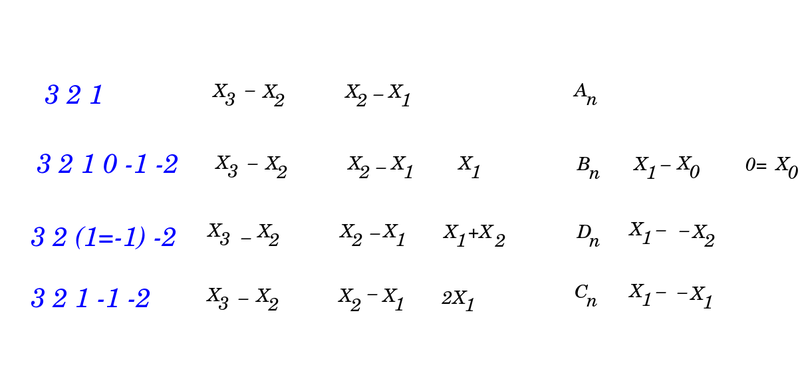
Visa tai turint omenyje, dabar paaiškinsiu, kaip galima suprasti klasikinių Lie algebrų šaknų sistemas. Galime jų paprastasias šaknis {$x_2-x_1$}, {$x_3-x_2$} ir taip toliau suprasti, kaip koduojančius skaičiavimą, 1, 2, 3 ir toliau iki skaičaus n. A šeima skaičiuoja toliau, {$x_{n+1}-x_n$}. Įsidėmėkime, yra dualizmas, kuriuo iš vieno galo skaičiuodami pirmyn 1, 2, 3 tuo pačiu iš kito galo skaičiuojame atgal -3, -2, -1. Ir įsivaizduokime, kaip senovės istorikams teko susitarti, kaip sudurti metų skaičiavimą pirmyn mūsų eroje su metų skaičiavimu atgal prieš mūsų erą. Tad trys klasikinės šeimos skirtingais būdais sprendžia, kaip sieti tokias dvi skaičiavimo kryptis. B šeima įveda papildomą, išorinį nulį, tuštumą, {$x_0=0$}, taip kad skaičiavimas vyksta -2, -1, 0, 1, 2. Pereinama iš 0 į 1, užtat atsiranda papildoma šaknis {$x_1-x_0=x_1$}. Galime įsivaizduoti, kad siūlo galus pririšome prie to išorinio nulio. D šeima apibrėžia vidinį nulį sutapatinant -1 ir 1, taip kad skaičiavimas vyksta -3, -2, -1=1, 2, 3. Pereinama iš -2 į 1, užtat atsiranda papildoma šaknis {$x_1-(-x_2)=x_1+x_2$}. Siūlo galus sulydėme. O C šeima tiesiog suduria abu skaičiavimus: -2, -1, 1, 2. Pereinama iš -1 į 1 užtat atsiranda papildoma šaknis {$x_1-(-x_1)=2x_1$}. Galima sakyti, siūlą tiesiog sulankstėme.
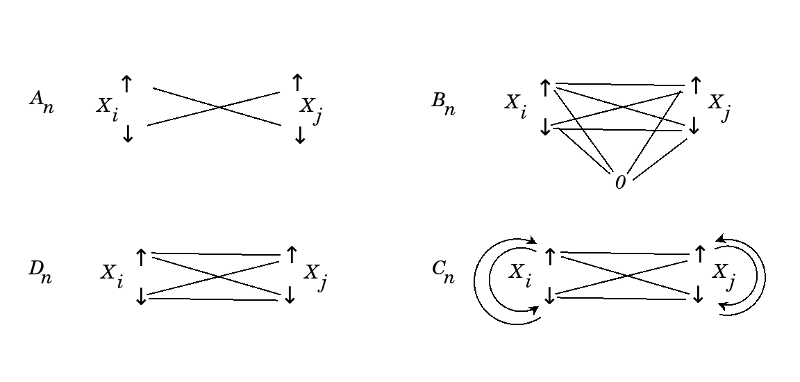
Dabar pasižiūrėkime į šias šaknų sistemas truputį kitaip ir suprasime kaip jos atitinka keturias sandaugų simetrijas. Įsivaizduokime, kad kiekvienas indeksas turi dvi angas, kairę ir dešinę. Šaknį galime laikyti taku tarp dviejų indeksų. A šeima griežtai skiria angas, taip kad vieni takai keliauja iš kairės į dešinę, o kiti takai keliauja iš dešinės į kairę. D šeima neskiria angų, taip kad galima keliauti iš kairės į kairę, iš kairės į dešinę, iš dešinės į kairę, ir iš dešinės į dešinę. B šeima yra panaši, tik jinai dar ir takus iš kiekvieno nario kairę į nulį. Nulio kairė ir dešinė sutampa, tad sutampa atitinkantys takai. Galiausiai C šeima yra panaši į D šeimą, tik jinai prideda taškus iš kiekvieno nario kairę į savo dešinę, ir iš kiekvieno nario dešinę į savo kairę. Užtat būtent C šeimoje einant tokiu iš nario į save apsisuka skaičiavimo kryptis. Tuo tarpu A šeimoje skaičiavimo kryptys griežtai skiriamos, o B ir D šeimose jos neskiriamos.
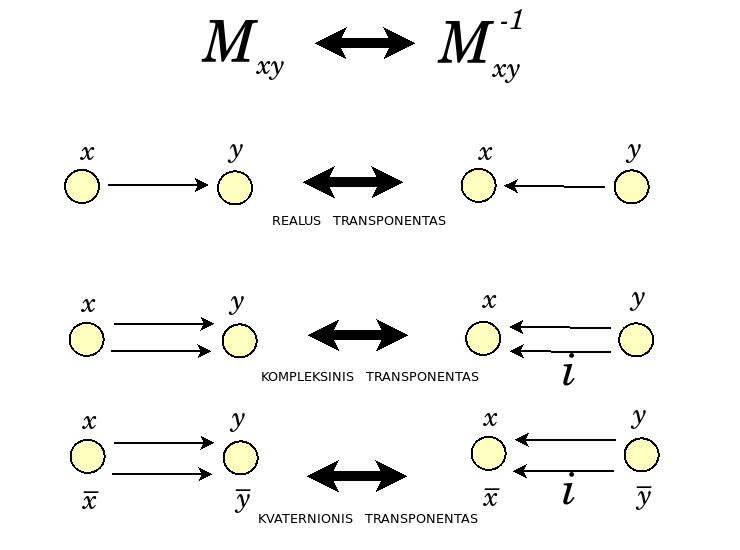
Įdomu, kad panašūs takai įžvelgtini interpretuojant Lie grupių matricų atvirkštines. Lie grupių matricos išsako posūkius. Ortogonalinės matricos nusako posūkius realiųjų skaičių erdvėje. D šeimai priklauso porinių dimensijų ortogonalinės matricos, o B šeimai priklauso neporinių dimensijų. Poriškumas ir neporiškumas iškyla dėl to nuliaus nebuvimo ar buvimo. A šeimai priklauso unitariosios matricos, nusakančios posūkius kompleksinių skaičių erdvėje. C šeimai priklauso simplektinės matricos, nusakančios posūkius kvaternionų erdvėje.
Posūkių matricos determinantas yra vienas. Tai reiškia, kad Kreimerio taisykle apskaičiuojant atvirkštinę, nereikia rūpintis vardikliu, yra tik skaitiklis, kas kombinatorikai itin dėkinga. Iš tiesų, posūkių matricų stulpeliai ir eilutės yra, kaip vektoriai, tampriai susiję. Realiųjų skaičių atveju stulpeliai ir eilutės yra ortonormiški. Užtat ortogonalinės matricos atvirkštinė prilygsta transponuotai matricai. Unitariosios matricos atvirkštinė yra kompleksiškai jungtinė ir transponuota matrica. Supraskime matricos narį kaip taką iš indekso i į indeksą j. Ortogonalinės matricos atveju, atitinkamas atvirkštinės narys išsakys taką atgal iš indekso j į indeksą i. Unitariosios matricos atveju teks papildomai parinkti kompleksišką jungtinę, kas išlaiko skirtumą tarp dviejų krypčių. Simplektinės matricos atveju matricas pasidalina į 2x2 kvadratėlius. Kvadratėlis nusako keturis takus tarp dviejų indeksų turinčių po dvi angas. Du takai veda iš kairės į dešinę ir iš dešinės į kairę. Tiesiog pakeičiame jų kryptį. Likę du takai veda iš kairės į kairę ir iš dešinės į dešinę. Mes taipogi pakeičiame jų kryptį, tačiau taip pat padauginame iš -1, kaip dera skiriant kompleksines jungtines. Tokiu būdu šie keturi takai pasidalina kaip kad kvarternionas pasidalina į du kompleksinius skaičius, nusakančius poziciją ir judesio kiekį, taip kad atvirkštinė išsako kvaternioniškai jungtinę ir transponuotą matricą.
Visa tai apžvelgiant, sakyčiau, kad A šeima išreiškia simpleksų simetriją ir kompleksiniais skaičiais griežtai skiria skaičiavimą pirmyn ir atgal, tarp židinio kuriame nieko nėra ir visumos, kuriame yra viskas. D šeima išreiškia koordinačių sistemų simetriją, tarsi reliatyvų kubą, ir savo reliatyvumu neskiria skaičiavimo pirmyn bei atgal. B šeima išreiškia hiperkubus, skaidančius absoliučią visumą, kuris yra tasai jų papildomas nulis, tačiau galima sakyti, nuo tos visumos skaičiuoja tiktai atgal, užtat išsikvepia. Šios dvi šeimos panaikina skaičiavimo krypčių skirtumą, iš kompleksinių skaičių padaro realiuosius skaičiau. Tuo tarpu D šeima išreiškia kryžminius politopus, kaip kad ortohedrą, kuriais galima skaičuoti pirmyn iš židinio ir pasiekti ją supančią plokštumų, langelių dangą, skiriančią vidų ir išorę, taip kad galima praplėsti skaičiavimą, jį pasukant pirmyn ir atgal, ir tokiu būdu kvaternionais praplėsti kompleksinius skaičius. Toliau bandyčiau susieti šias keturias simetrijas, šias klasikines šeimas, su keturiomis geometrijomis: projektyvine, afinine, konformalia ir simplektine.
Ačiū Rimvydui Krasauskui už pabendravimus šiais klausimais.
Žr. Santrauka, Juodraštis
LieSandarųIštakos
Recent Changes
网站
Įvadas #E9F5FC
Klausimai #FFFFC0
Teiginiai #FFFFFF
Kitų mintys #EFCFE1
Dievas man #FFECC0
Iš ankščiau #CCFFCC
Mieli skaitytojai, visa mano kūryba ir kartu visi šie puslapiai yra visuomenės turtas, kuriuo visi kviečiami laisvai naudotis, dalintis, visaip perkurti. - Andrius