Dabartinė estetika ir meno filosofija: tarp tradicijos ir inovacijų. 2016 m. birželio 11–12 d.
Matematikos grožis žadina vaizduotę
http://www.youtube.com/watch?v=k2wMoe3utfw
Dviem pavyzdžiais iš matematikos jums parodysiu, kaip pilnatvė reiškiasi grožiu.
Pirmiausia, kalbėsiu kaip pilnatvė veikia mūsų jausmus. Pilnatvę įsivaizduoju kaip ramybę iš kurios viskas išplaukia. Manau, ją suvokiame klausimu kodėl ir atsakymu todėl, jų vidine kūrybine įtampa.
Prieš dvejus metus šioje konferencijoje kalbėjau apie kūrybos prasmę ir meno taisykles. Kūrybos prasmė, tai radimas ką veikti su savo laisve, o tuo pačiu, ko veikti, atradimas kodėl? Gyvenime dažnai atitrūkstame nuo to požiūrio, kodėl. Grožyje įžvelgiame, kad toksai kodėl yra. O kūryba tą kodėl įkūnijame, įvaldome, įgyvendiname.
Tačiau mūsų kūryba yra ribota. Mes viską bandom įsprausti į betką. Dievas trokšta betko, jisai ramus, tuo tarpu mes gyvename lūkesčiais, iš kurių išplaukia visi mūsų jauduliai bei jausmai, įskaitant ir žavesys.
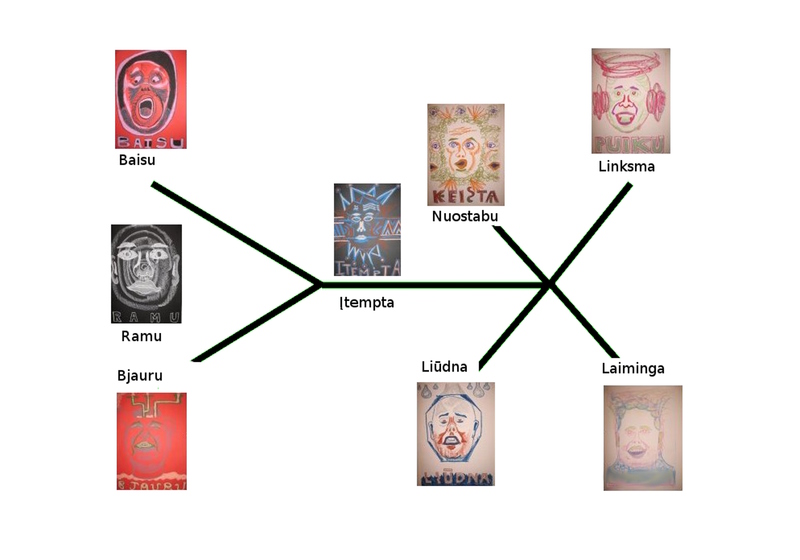
Įsivaizduokime mergytę žaidžiančią su kaladėlėmis. Ji mato raidę užrašytą kaladėlės viršuje ir bando atspėti, kokia raidė užrašyta kaladėlės apačioje. Tarkim ta kaladėlė jai svetima, nelabai pažįstama. Jeigu jinai teisingai atspės, jinai pralinksmės, o jeigu neteisingai atspės, jinai nustebs. Dabar jeigu ta kaladėlė jai artima, gerai žinoma, jeigu pasitvirtins, jog yra taip, kaip turi būti, jinai pasijus laiminga, patenkinta, nuraminta, jog viskas gerai. Tačiau jeigu paaiškės, kad jinai žiauriai klysta, tai jinai susigraudens, kaip jos mėgstamioji kaladėlė galėjo ją taip išdurti.
Kolei jinai laukia atsakymo, jinai jaučia įtampą, nežinią. Tačiau tarkim ją ištinka tai ko ji negali, nenori ar nesutinka tikėtis. Jeigu tai kyla iš lauko, iš to kas jai svetima, tai jai baisu. O jeigu tai ateina iš vidaus, iš to kas jai sava, tai jai bjauru.
Visi septyni jauduliai - laimė, liūdesys, linksmumas, nuostaba, baimė, bjaurumas, įtampa - tėra jos lūkesčių atspindžiai tikrovės šviesoje. Be lūkesčių jinai gyventų rami. Jėzus kaip tik linkėdavo ne laimės, o ramybės.
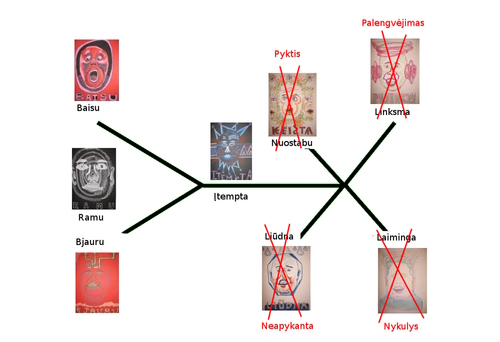
Jeigu mes laukiam to, ko netrokštam, tada viską išgyvename neigiamai. Kada mus ištinka tai, ko laukėme, bet nenorėjome, tada pykstame arba netgi neapkenčiame, kad taip pasitvirtino. O jeigu neįvyksta, tai geriausiu atveju, pajuntame palengvėjimą, tačiau kada mums reikalas asmeniškai svarbus, tada mums nyku, kad atsisakėme laimės, kad nesiryžome tikėtis to, ko iš tiesų norėjome.
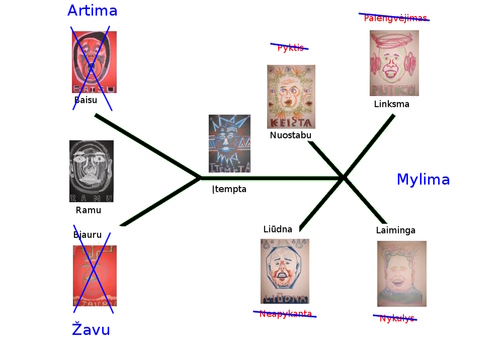
Ramybės kūryba vyksta tokiais lūkesčiais, kuriais laukiame ko trokštame, kuriais gyvename ramūs, jautrūs, teigiami. Tiek laimė, tiek liūdesys yra ženklai, jog mūsų lūkesčiai teisingi, esame viena, gyvename pilnatve. Yra trys pilnatvės dorybės - žavesys, artimumas ir meilė - kurios pašalina bjauresio, baimės ir neapykantos sąlygas. Meilė įžvelgia pilnatvę mūsų troškimuose, taip kad neigimas pats paneigtinas, nėra prasmės netikėti, nėra reikalo neapkęsti. Artimumas įžvelgia pilnatvę mūsų visų gelmėse, taip kad mūsų išorinis gyvenimas bereikšmis ir nėra ko bijoti. O žavesys įžvelgia pilnatvę už mūsų, taip kad mūsų vidinis gyvenimas tampa bereikšmis ir nėra ko bjaurėtis.
Žavesys tad yra mūsų jausmų raktas, kuriuo linksmi ar nustebinti įžvelgiame pilnatvę už mūsų. Vienu tyrų tyriausiu matematikos pavyzdžiu stebėkime pilnatvės kūrybą, o paskui pačiu įmantriausiu matematikos pavyzdžiu atpažinkime pilnatvės kūrinius.

Įsivaizduokime lauką ir jame laukime - tai susiję žodžiai. Laukiame, kad pilnatvė, esanti už bet kokių ribų, už mūsų jausmų ir mūsų pačių, visgi pasireikštų mūsų erdvėje ir laike, tai yra, mūsų vaizduotėje. Ką jinai gali mūsų vaizduotėje sukurti ir kaip jinai gali mūsų vaizduotę atverti? Jinai trokšta nieko - savarankiška, pirmapradė; jinai trokšta kažko - užtikrinta, dėmesinga; jinai trokšta betko - rami, dviprasmiška; jinai trokšta visko - mylinti, kurianti.
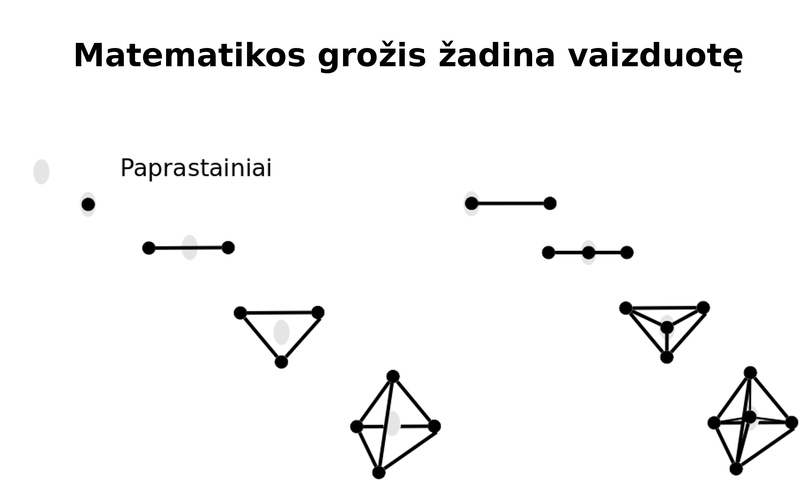
Papasakosiu tokį pilnatvės apsisukimą kuriuo jinai sutveria begalinę šeimyną sandarų, kuriais matematikai tiria vaizduotės erdves. Matematikai šiuos geometrijos pradus vadina simpleksais, tačiau aš lietuvių kalba juos pakrikštysiu paprastainiais.
Įsivaizduokime pilnatvės vidinę įtampą. Ar jai reikštis ar nesireikšti? Yra būtent tai, kas reiškiasi. Ar jai būti ar nebūti? Ar ji iš viso būtina? Ar ji būtų netgi jeigu jos nebūtų? Tokiais klausimais, troškimais, tokia įtampa, pilnatvė susitelkia į lauko židinį, kol kas nematomą, visgi vaizduotėje labai ryškų.
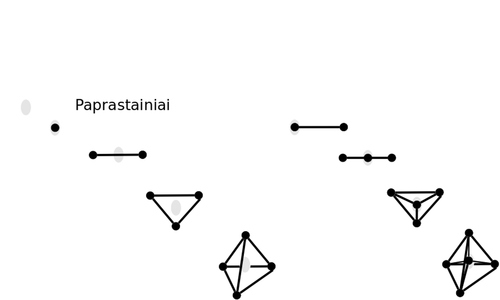
Toliau pilnatvė pasireiškia. Jinai išeina už savęs į save, į lauką, kuriame pasirodo tašku. Tai mūsų paprastainis, kol kas nulmatis.
Židinys sutampa su tašku, tarsi atsivėrusi akis, ir kaip jos laisva dvasia, slenka pirmyn ir atgal, ir galiausiai sukuria naują, susijusį tašką. Ji tokiu būdu atveria naują matą, sukuria jau vienmatį paprastainį, kraštinę, kurioje naujai įžvelgtinas pilnatvės židinys.
Dabar galime įsivaizduoti, jog tos kraštinės židinys įsismaginęs kyla ir krenta ir kyla, taip kad iškyla dvimatis paprastainis, lygiakraštis trikampis, visai juokingai, tarsi palapinė. Pasižiūrėjus iš šono trikampyje naujai įžvelgiame židinį.
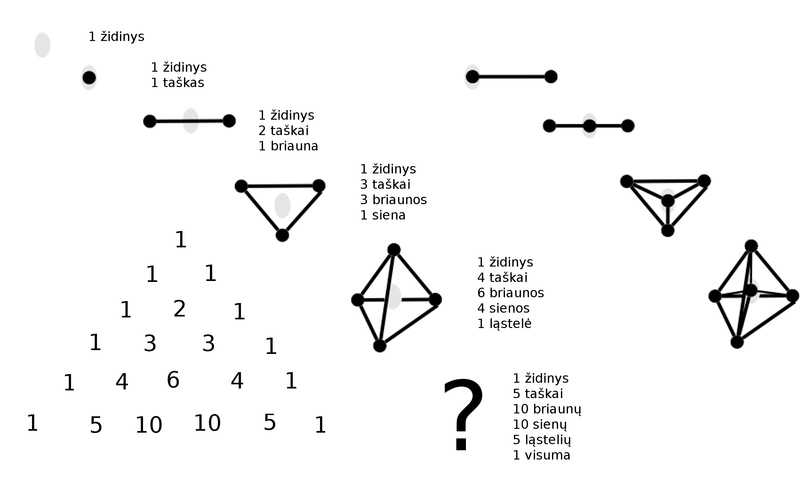
Ir vėl įsivaizduokime, kaip židinys atveria naują matą, tampa tašku ir sukuria jau trimatį paprastainį, tetraedrą, piramidę sudarytą iš trikampių. Matematikė pastebi, jog šis paprastainis turi vieną židinį, keturias viršūnes, šešias briaunas, keturias sienas ir vieną visumą. Šie skaičiai dėsningai išplaukia iš sandaugos kuria kiekviena dalis kiekvieną tašką pasirenka ar nepasirenka. Matematikė šiuos skaičius gerai išmano ir gali pasakyti, kad keturmatis paprastainis turės vieną židinį, penkias viršūnes, dešimt briaunų, dešimt sienų, penkias ląsteles ir vieną visumą.
Įpaišydami piramidės židinį galime kaip tik įžvelgti šį keturmatį paprastainį, ketvirmačio pasaulio būtybę! Galim nupaišyti ir suskaičiuoti jos kraštines ir šonus. Galim įsivaizduoti, kaip židinys slankioja mums nematomu ketvirtu matavimu. Galim per piramidės keturias sienas išversti keturias ląsteles, tai yra, keturias papildomas piramides, ir stebėtis, kaip penkios piramidės sudaro keturmatį paprastainį.
Žodžiu, užtenka penkių taškų išsivaduoti iš mūsų vaizduotės trimačio kalėjimo. Pakanka keturių taškų grožėtis piramidės didybe, trijų taškų nusijuokti, kaip trikampis atrodo iš viršaus, dviejų taškų pašalinti vienatvę, vieno taško įžiebti gyvybę ir betaškio židinio atpažinti Dievą ir jo kūrybą. Ir kiekvienas naujas taškas matematikei laimi naują visatos matmenį, naujų jausmų, iki begalybės.

Paprastainių raida puikiai pavaizduoja architekto Kristoferio Aleksandro knygoje "Tvarkos prigimtis" apibūdintą pilnatvę skleidžiančią kūrybą ir ypač tris pagrindines gyvybės raiškas: ryškūs židiniai, aiškios ribos ir laipsningi mąstai. Kitu, įmantresniu matematikos pavyzdžiu, pristatysiu dar dvylika jo pastebėtų gyvybės raiškos dėsnių. Tai fraktalas, Mandelbroto aibė, kurią pavadinsiu Musgaudžio rinkiniu.
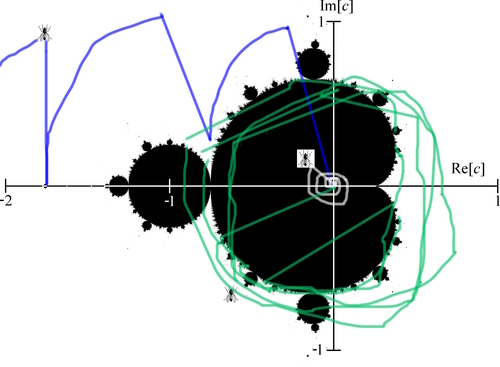
Įsivaizduokime plokštumą. Apytikriai paaiškinsiu kokiu būdu spręndžiamas ar plokštumos taškas priklauso Musgaudžio rinkiniui ar ne. Mums rūpimas taškas apibrėžia tam tikrą kryptį ir nuotolį nuo plokštumos pradžios, tai yra, jos židinio. Įsivaizduokime, kad kaskart musę pabaidome musiamušiu ta pačia kryptimi ir tą patį nuotolį. Tačiau savo ruožtu jinai kokį kampą ratu apskridusi apie židinį, tokį jinai kampą dar apskris. Jeigu jinai arti židino, tai priskris dar arčiau - kvadratu, o jeigu jinai nutolusi, tai dar toliau - irgi kvadratu. Žiūrim, kuom viskas baigsis. Jeigu musė išlėks į tolumas, tai taško neįskaitysim į Musgaudį ir jį nuspalvinsim mėlynai. Jeigu jinai priskris prie židinio, tai tašką nuspalvinsim juodai. O jeigu jinai amžinai lekios aplinkui, tai tašką nuspalvinsim dar kokia spalva. Čia jau bus menininkų skonio reikalas.

Dabar nersime gilyn į šį be galo painų taškų rinkinį. Jame įžvelgsime dvylika gyvybės raiškų ir dvylika menininkų nuostatų, kuriuos pristačiau prieš dvejus metus. Žavėsimės ne kūryba, kaip matematikai, o kūriniais, kaip menininkai. Tačiau ir čia pastebėsime, kaip pilnatvė reiškiasi įvairiausiomis priešingybėmis, jomis sukuria lauką gyvybei.


Menininkė pristato tikrovę. O tam reikia išlaisvinti priėjimą. Jaučiame įtampą tarp buvimo ir nebuvimo. Dėmesys tuštumai leidžia statiniams iškilti, išsiplėtoti.

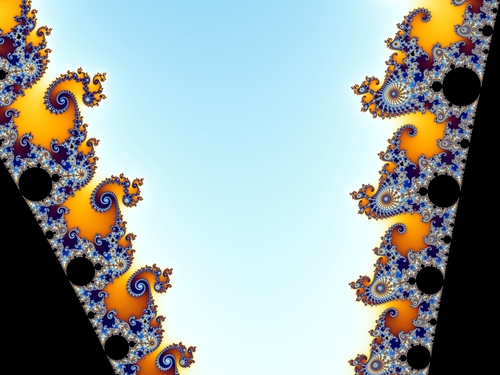


Toliau, menininkė priešpastatydama iškelia tai, kas nepastebėta. Išryškina savybių priešingybes. Pavyzdžiui, vienas židinys apvalus, kitas kampuotas.


Menininkė atveria galimybes kaitaliojimu. Panašiose aplinkybėse viena kūrybinė jėga išgauna vienokias pasekmes, kurios visos kartu sudaro aplinkybes visai priešingai jėgai. Viena jėga krauna kopas, kita tarp jų kasa duobes. Dvi jėgos kartu išvysto aiškius pavidalus.


Menininkė įkvėpia kurti, tad sveikai dalina erdvę, ją ruošia kitų židiniams. Bręstantys židiniai ir būsimi židiniai ištempia ribas ir išskaido erdvę.


Menininkė lavina jautrumą nuotaikoms, tad pina daugiaprasmybę. Atsitiktiniai virpesiai išsididina dviprasmiškais ribos židiniais, susiskambančiais su priešingų kraštų židiniais.


Menininkė tiesą įamžina kūrinyje, tad sustato taisyklingą pavidalą. Kampais išryškina ribas, taip kad susigaudome, kas vidus ir kas išorė.
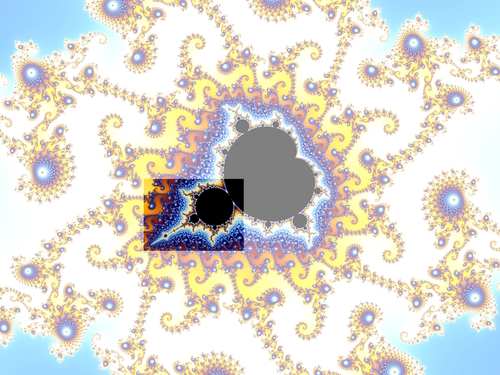
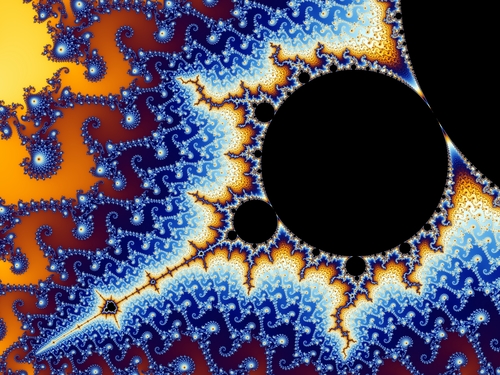
Menininkė kalba sąvokomis, tad išsireiškia grubiai, dalykiškai. Jaučiam faktūrą, įtampą tarp suvokiamumo ir nesuvokiamumo. Didelės, dėsningos jėgos verčia smulkesnes jėgas įvariausiai derintis, tarsi atsitiktinais, netikėtais, nesuvokiamais sprendimais.
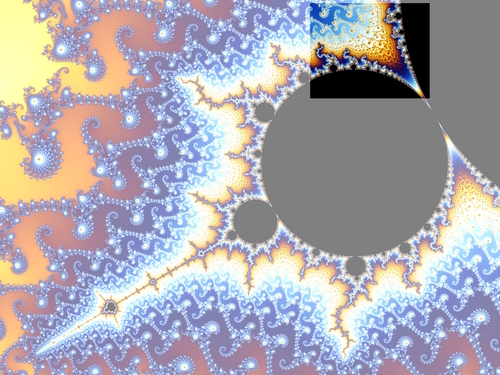
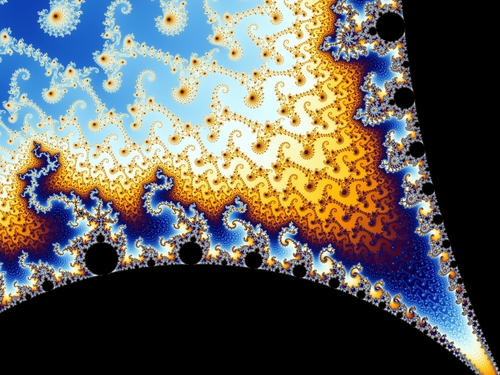
Menininkė įsijaučia į savo vaidmenį. Ji kūrinį supaprastina ir pati nurimsta. Atsisako visko, kas nereikalinga, išryškina tai, kas reikalinga. Išvalo tai, kas niekam netarnauja, kas be tikslo.
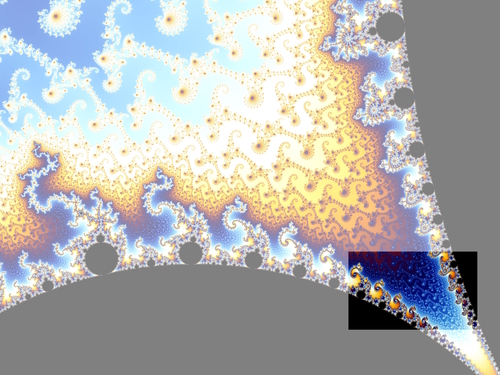
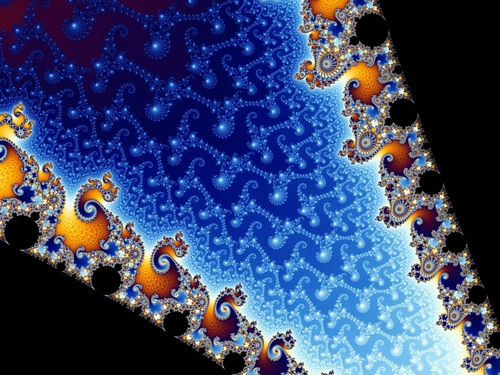
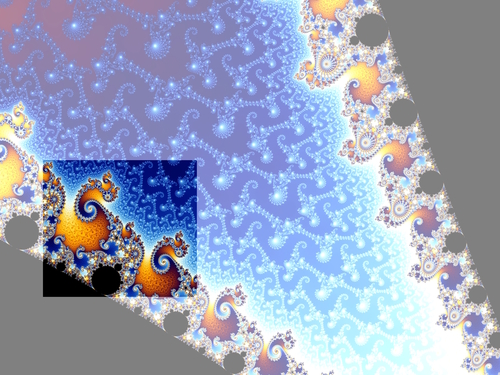

Menininkė tampa ir gyvena kuo tikrai yra. Jinai išpildo erdvę, švelnina skirtumą tarp vidaus ir išorės, židinius apsupa židinėliais, sieja sąsajomis.
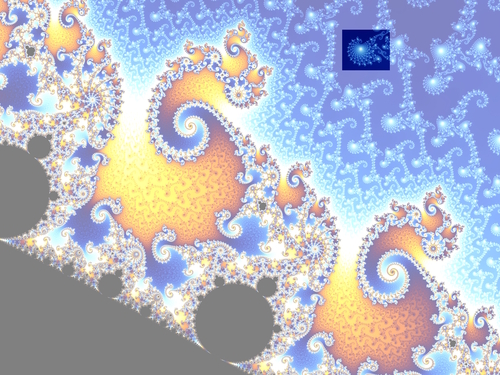

Menininkė gyvena meno įrankiu. Jinai kryptingai ryškina židinį ir lauką, tolydžia kaita išreiškia židinio trauką.


Menininkė pasimeta kūrybos džiaugsme. Jos kūryba aidi. Panašūs veiksmai skamba panašiose aplinkybėse, tad kartojasi panašūs padariniai.

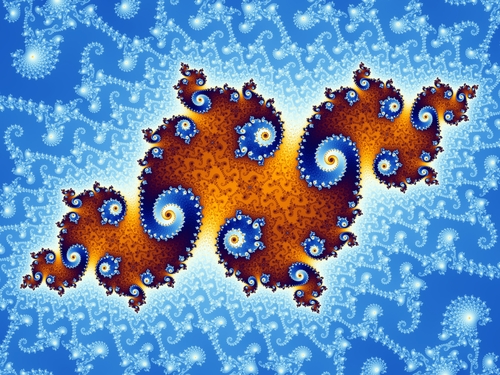
Menininkė pasaulį perkuria, tad jinai kloja simetrišką dugną. Židinio ir lauko tvarus santykis grindžia simetriškumą, įtvirtina židinį, išryškina lauko galimybes.
Aš tikiu, kad iš šių dviejų matematikos pavyzdžių ir taip pat iš jaudulių bei jausmų aptarimo galime pamanyti, kad iš tiesų pilnatvė dėsningai plėtojasi mūsų vaizduotėje, matematikoje, visatoje, gamtoje, menuose, bet kokioje kūryboje. Galime kartu su architektais Kristoferiu Aleksandru ir Bukminstru Fuleriu rinkti pilnatvės plėtros pavyzdžius, jos dėsnius išryškinti ir taikyti menais bei mokslais.

Abiejuose pavyzdžiuose pilnatvės plėtra reiškiasi priešingybėmis. Kūryboje, vaizduotėje, pilnatvė sau priešpastato židinį, židiniui tašką, taškui laisvumą, laisvumui židinį. Pilnatvė palaiko visatos ir meno kūrinių gyvybę išryškindama vis naujas priešingybes, tad vis naujas dviprasmybes. Galime nagrinėti, kurios priešingybės ryškina židinėlius, jų samplaikas, ištisą kūrinį ar netgi patį Kūrėją, pilnatvę, išeities tašką, Kodel.
Žavesys tačiau tėra viena iš trijų pilnatvės išraiškų, ta išmintis kuri pakilusi virš mūsų, kuri žadina nuostabą bei jaudulį, ir kviečia mąstyti. Artimumas yra pilnatvės išraiška siejanti mūsų gelmes, žadinanti džiaugsmą ir liūdesį, kaip kad muzika, ir įkvėpia nusistatyti. O meilė, tai pilnatvės išraiška, kviečianti mus gyventi teigiamais lūkesčiais, su tikėjimu laukti, ko iš tikrųjų trokštame, to siekti, tai įgyvendinti.
MatematikosGrožisŽadinaVaizduotę
Recent Changes
网站
Įvadas #E9F5FC
Klausimai #FFFFC0
Teiginiai #FFFFFF
Kitų mintys #EFCFE1
Dievas man #FFECC0
Iš ankščiau #CCFFCC
Mieli skaitytojai, visa mano kūryba ir kartu visi šie puslapiai yra visuomenės turtas, kuriuo visi kviečiami laisvai naudotis, dalintis, visaip perkurti. - Andrius